最近刚好在做数字图像处理的实验课
记录一下简单处理图像的方法
顺便水贴
0×01一些基本操作
读入图像
imread(filename)
- filename–>图像路径
- 读入的图像是一个三维矩阵 img [row] [col] [rgb]
- 最里面的维度是RGB颜色通道,循序为[R-G-B]
- eg :
img = imread('C:\Users\Aov\Desktop\Matlab\A.jpg')
图像显示
imshow(img)
- img–>图像
- eg:
figure(2);imshow(img);title("This is a img")
图像放缩
imresize(img,scale)
- img –>图
- scale–>放大倍数,0到1缩小,大于1放大
- eg:
img = imresize(img,0.2)
转灰度图
作为智能车er,受限于主控性能,需要验证的大部分是灰度图。
rgb2gray(img)
- img–>RGB图像
- 返回的图像是灰度图像
- eg:
gray_img = rgb2gray(RGB_img)
gray = A*Red + B*Green + C*Blue
- 通过手动读取彩色图像的RGB三个通道并混合为一个,得到灰度图
%获取RGB单通道图像
Red = img(:,:,1);
Green = img(:,:,2);
Blue = img(:,:,3);
- ABC的取值有很多,例如
Gray = (Red + Green + Blue) / 3
Gray = (Red * 0.3 + Green * 0.59 + Blue * 0.11)
Gray = (Red * 0.2126 + Green * 0.7152 + Blue * 0.0722)
Gray = (Red * 0.299 + Green * 0.587 + Blue * 0.114)
- 上述方法都是得到正常灰度图的方法,如果芯片跑得动凌瞳这种彩色摄像头,处理又要处理灰度图,可以尝试改变ABC的比例得到不正常的灰度图。
- 比如正常的蓝白赛道可以取蓝色的通道为零 即
A=0.5 B=0.5 C=0 ,可以看到蓝色的赛道黑了一点点

灰度直方图
imhist(gray_img)
- 灰度直方图是查看图像灰度分布非常直观的方法
- 横坐标是像素值从小到大的排列
- 纵坐标是像素值在图像中的个数
- 如果二值化可以很方便的找到阈值
- eg:
imhist(img);

获取图像长宽
[ROW,COL] = size(gray_img)
size()函数用来获取矩阵每一维度的长度,n维矩阵返回n个值。- 这里默认了图象是灰度图,只有一个色彩通道,是一个二维矩阵
图像二维卷积
conv2(N1,N2,shape)
- MATLAB提供的二维卷积
N1 –> 图像N2 –> 卷积核shape –> 'full' 'same' 'valid'
full: 滑动步长为1,图片大小为N1xN1,卷积核大小为N2xN2,卷积后图像大小:N1+N2-1 x N1+N2-1same: 滑动步长为1,图片大小为N1xN1,卷积核大小为N2xN2,卷积后图像大小:N1xN1valid:滑动步长为S,图片大小为N1xN1,卷积核大小为N2xN2,卷积后图像大小:(N1-N2)/S+1 x (N1-N2)/S+1
- 参考(https://www.cnblogs.com/hyb221512/p/9276621.html)
或者闲的*疼 运用矩阵 · 乘 再求和手动卷积
获取均值
mean(A)
A–>向量或矩阵- 多维矩阵返回均值向量
- 向量返回均值值
排序
sort(A)
B = sort(A) : 多维矩阵返回排列后的矩阵;向量返回排列后的向量[B,id] = sort(A) : 返回排列后矩阵时还会带有原本的索引值
0×02图像的灰度变换
线性动态范围调整
公式
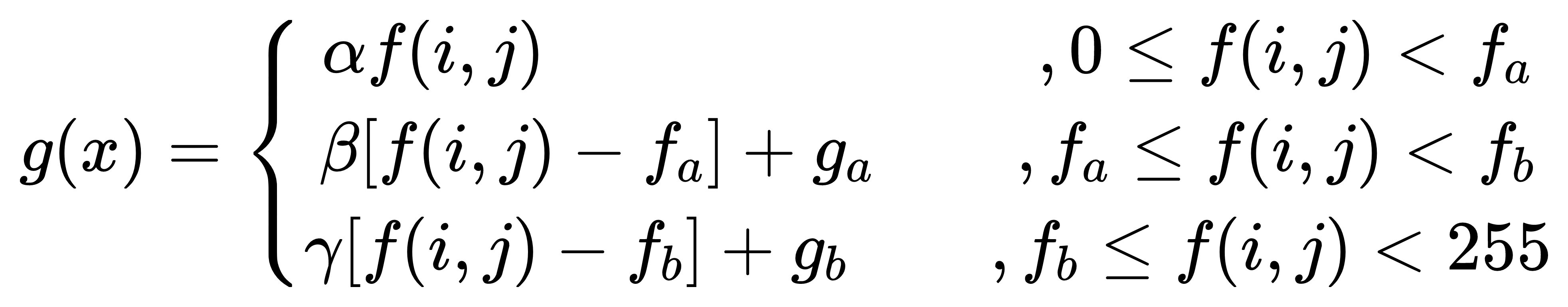
映射曲线
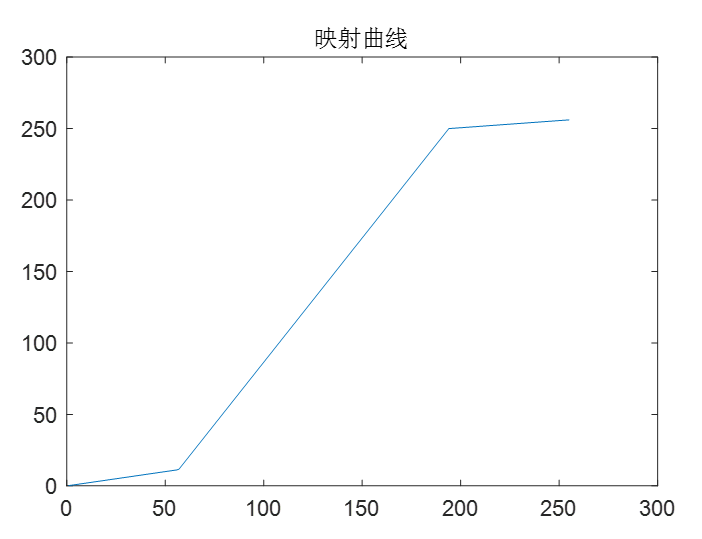
- 横坐标是原图的灰度值 纵坐标是输出图像的灰度值
- 可以看到对于中间的一段区间 其灰度区间线性放大了,效果上对比度提升
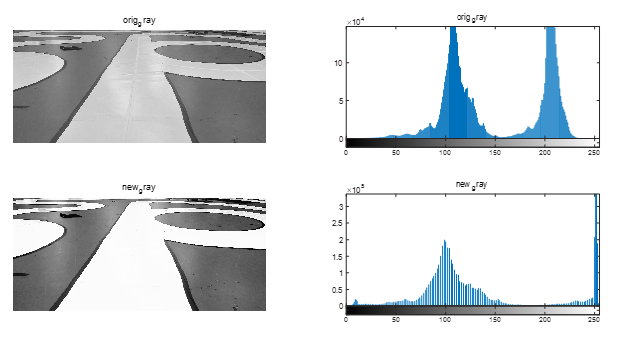
%read img
pic = imread('C:\Users\jason\Desktop\Matlab\A.jpg');
%2gray
orig_pic = rgb2gray(pic);
%2double
imshow(orig_pic)
gray_pic = double(orig_pic);
%get max min
pic_max = max(max(gray_pic));
pic_min = min(min(gray_pic));
%get abcd
a = double(pic_min+50);
b = double(pic_max-50);
c = double(10);
d = double(250);
%for
[row,col] = size(gray_pic);
new_pic = zeros(row,col);
for y = 1:row
for x = 1:col
if gray_pic(y,x)<=a
new_pic(y,x) = (c/(a-pic_min))*gray_pic(y,x);
elseif gray_pic(y,x)<=b
new_pic(y,x) = ((d-c)/(b-a))*(gray_pic(y,x)-a)+c;
elseif gray_pic(y,x)>b
new_pic(y,x) = ((255-d)/(pic_max-b))*(gray_pic(y,x)-b)+d;
end
end
end
%2uint8
new_pic = uint8(new_pic);
gray_pic = uint8(gray_pic);
%show
subplot(221); imshow(orig_pic);title("orig_gray");
subplot(222); imhist(orig_pic);title("orig_gray");
subplot(223); imshow(new_pic);title("new_gray");
subplot(224); imhist(new_pic);title("new_gray");
%映射曲线
y = ones(1,255);
for i = 1:255
if i<=a
y(i)=(c/(a-pic_min))*i;
elseif i<=b
y(i)=((d-c)/(b-a))*(i-a)+c;
elseif i>b
y(i) = ((255-d)/(pic_max-b))*(i-b)+d;
end
end
i = 0:256;
figure(3);plot(y);title("映射曲线");
非线性动态范围调整
公式:
![[QianJianTec1684916301286.jpg]]
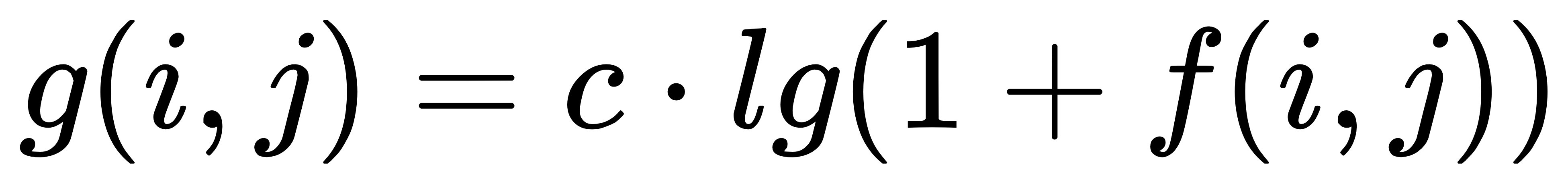
- 参数
c的确定可以带入f(i,j)的最大值和g(i,j)期望的最大值到f(i,j)和g(i,j),例如255 = c*lg(1+240)反解出c
映射曲线:
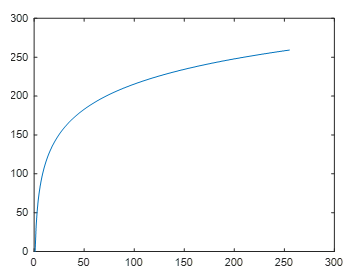
效果:
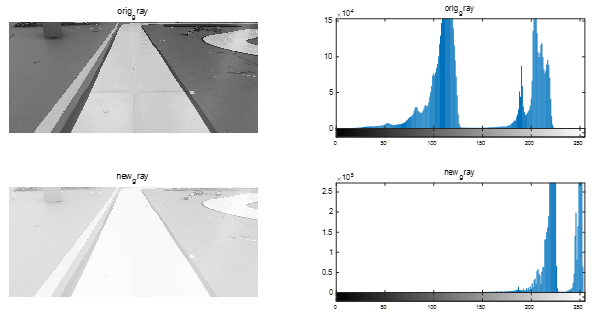
- log非线性映射经常作用在图片很暗的情况,可以把图片暗部变亮并且分布范围扩大,同时亮部继续变量,分布范围被压缩。
代码:
%un-liner transform
%read img
pic = imread('B.jpg');
%2gray
orig_pic = rgb2gray(pic);
%2double
imshow(orig_pic)
gray_pic = double(orig_pic);
%get max min
pic_max = max(max(gray_pic));
pic_min = min(min(gray_pic));
%get c
c = 255/log(1+pic_max);
%log
new_pic = c*log(1+gray_pic);
%2uint8
new_pic = uint8(new_pic);
gray_pic = uint8(gray_pic);
%show
subplot(221); imshow(orig_pic);title("orig_gray");
subplot(222); imhist(orig_pic);title("orig_gray");
subplot(223); imshow(new_pic);title("new_gray");
subplot(224); imhist(new_pic);title("new_gray");
figure(2);
i = 1:255;
plot(c*log(i));
title("映射log曲线")
直方图均衡化
- 看名字就只知道 最终目的是将灰度直方图摊开,各个像素灰度概率均衡
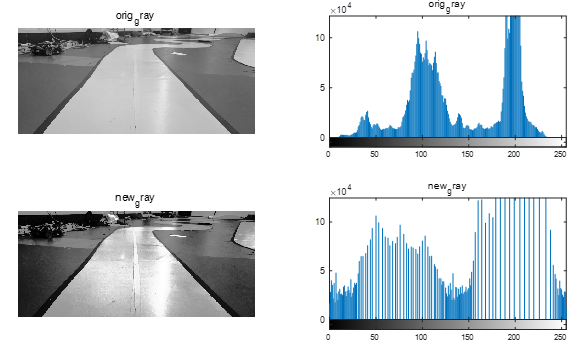
- 上图的原图中像素集中的地方在变换后平均分布在灰度直方图上
- 具体的处理流程 见
《数字图像处理》朱虹 著 P43-46 懒.jpg
- 大概是
- 求灰度直方图,用向量
hf表示
- 由直方图求灰度分布概率
pf = hf/Nf (Nf为像素个数)
- 计算累计分布概率
pa
- 像素计算
g(i,j) = 255*pa(k)
代码:
%zhifangtu transform
%read img
pic = imread('C.jpg');
orig_pic = rgb2gray(pic);
%2double
gray_pic = double(orig_pic);
%get max min
pic_max = max(max(gray_pic));
pic_min = min(min(gray_pic));
%get row col
[row,col] = size(gray_pic);
%get Pf Pa
pix_num = ones(1,256);
for i = 1:256
[n,nn]=find(orig_pic==(i-1));
pix_num(i)=length(n);
end
pix_num = double(pix_num);
pix_pf = pix_num/(row*col);
pic_pa = ones(1,256);
mid = 0;
for i =1:256
mid = mid + pix_pf(i);
if i~=0
pix_pa(i) = mid;
end
end
%show Pa
figure(1);
plot(pix_pa)
pix_pa = 255.*pix_pa;
%get pic
for y = 1:row
for x = 1:col
new_pic(y,x) = pix_pa(orig_pic(y,x));
end
end
%2uint8
new_pic = uint8(new_pic);
gray_pic = uint8(gray_pic);
%show
figure(2);
subplot(221); imshow(orig_pic);title("orig_gray");
subplot(222); imhist(orig_pic);title("orig_gray");
subplot(223); imshow(new_pic);title("new_gray");
subplot(224); imhist(new_pic);title("new_gray");
0×03 边缘检测
首先是内置函数edge(img,method)
edge_img = edge(Img,method) : 使用 method 指定的边缘检测算法检测图像 Img 中的边缘。- method–>
| 方法 | 描述 |
|---|
"Sobel" | 使用导数的 Sobel 逼近,通过寻找图像 I 的梯度最大的那些点来查找边缘。 |
"Prewitt" | 使用导数的 Prewitt 逼近,通过寻找 I 的梯度最大的那些点来查找边缘。 |
"Roberts" | 使用导数的 Roberts 逼近,通过寻找 I 的梯度最大的那些点来查找边缘。 |
"log" | 使用高斯拉普拉斯 (LoG) 滤波器对 I 进行滤波后,通过寻找过零点来查找边缘。 |
"zerocross" | 使用您指定的滤波器 h 对 I 进行滤波后,通过寻找过零点来查找边缘。 |
"Canny" | 通过寻找 I 的梯度的局部最大值来查找边缘。edge 函数使用高斯滤波器的导数计算梯度。此方法使用双阈值来检测强边缘和弱边缘,如果弱边缘与强边缘连通,则将弱边缘包含到输出中。通过使用双阈值,Canny 方法相对其他方法不易受噪声干扰,更可能检测到真正的弱边缘。 |
"approxcanny" | 使用近似版 Canny 边缘检测算法查找边缘,该算法的执行速度较快,但检测不太精确。浮点图像应归一化到范围 [0, 1]。 |
栗子:
- 使用了Robert、Prewitt、Sobel与log算子
- log算子等同高斯滤波后用Laplace
%edge
%read img
img = imread('B.jpg');
%2gray
gray = rgb2gray(img);
gray = imresize(gray,0.05);
%2double
gray = double(gray);
Roberts_o = edge(gray,'Roberts');
Prewitt_o = edge(gray,'Prewitt');
Sobel_o = edge(gray,'Sobel');
Laplace_o = edge(gray,'log');
%2uint8
gray = uint8(gray);
%show
subplot(321);imshow(img);title("Orig");
subplot(322);imshow(gray);title('Gray');
subplot(323);imshow(Roberts_o);title("Roberts");
subplot(324);imshow(Prewitt_o);title('Prewitt');
subplot(325);imshow(Sobel_o);title("Sobel");
subplot(326);imshow(Laplace_o);title('Laplace');
效果:
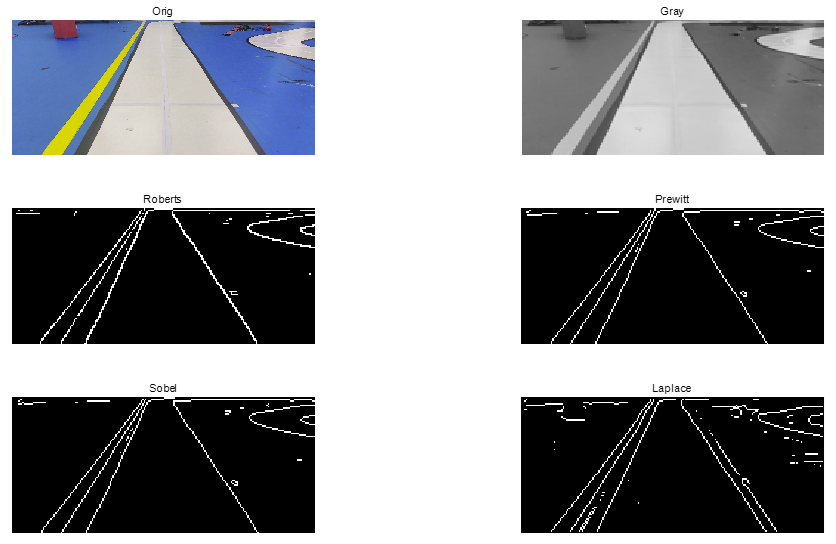
- 这些函数自带了一些参数与后处理,想在单片机上实现还要要求效率并不现实
- 图片尺寸缩小到了
92 * 205,与实际车车的相差不大
然后是:可以通过图像卷积函数conv2()手动卷积边缘检测算子
各个算子:
Roberts:
- Roberts算子是一种利用局部差分算子寻找边缘的算子。
- 边缘定位准,但对噪声敏感。适用于边缘明显而且噪声较少的图像分割,在应用中经常用Roberts算子来提取道路。
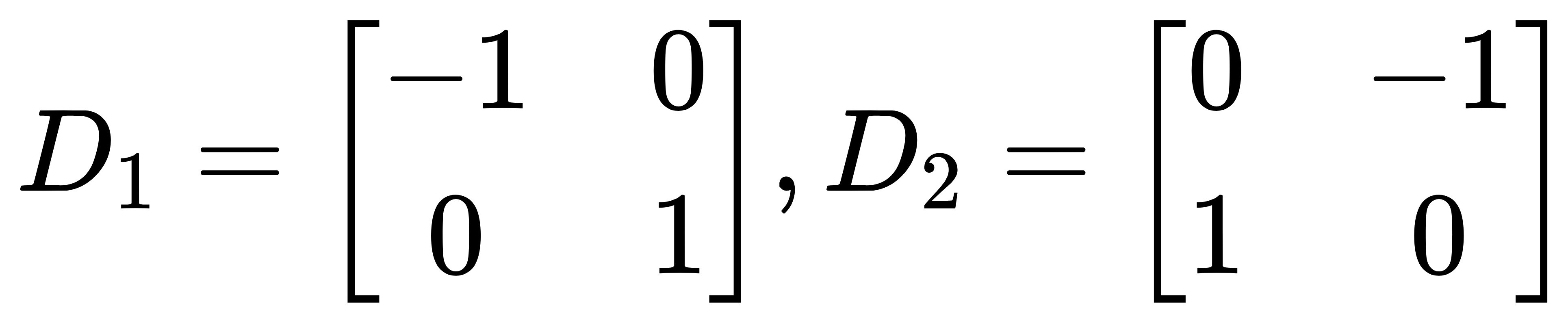
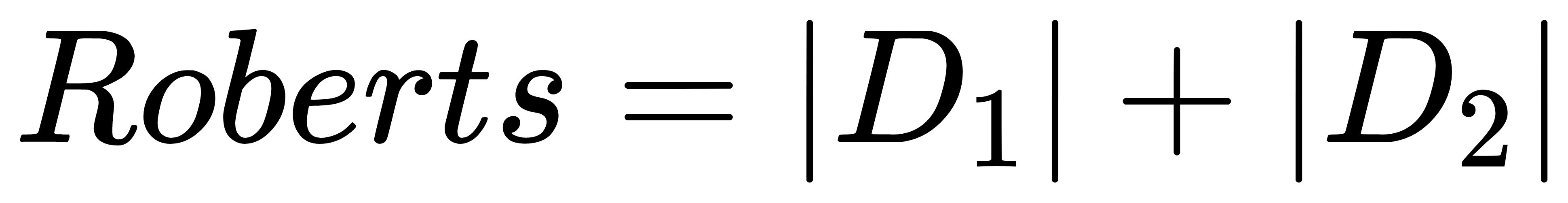
Sobel:
- Sobel算子包含两组3X3矩阵,分别为横向及纵向,将之与图像作平面卷积,即可分别得出横向及纵向的亮度差分近似值。
![[QianJianTec1684925004435.jpg]]
![[QianJianTec1684925565093.jpg]]
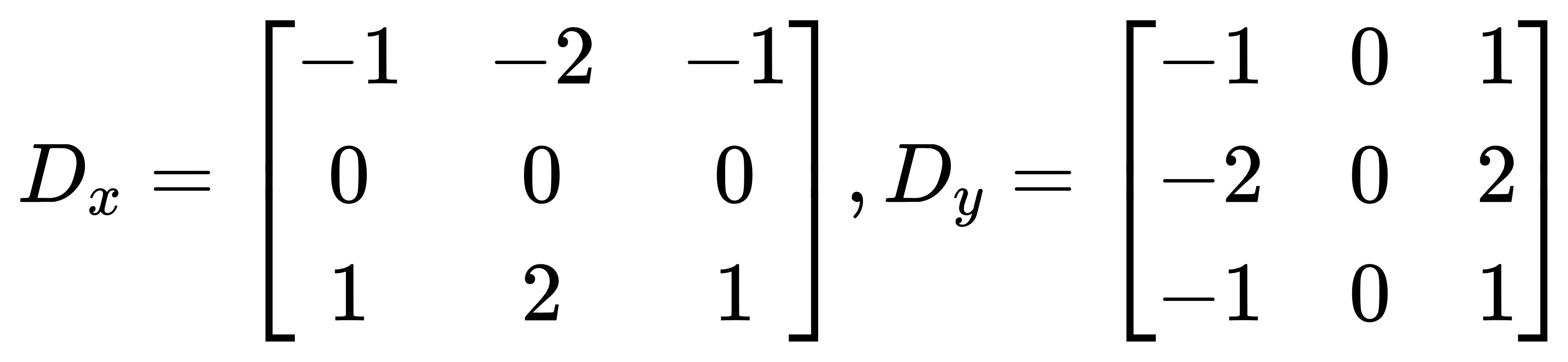
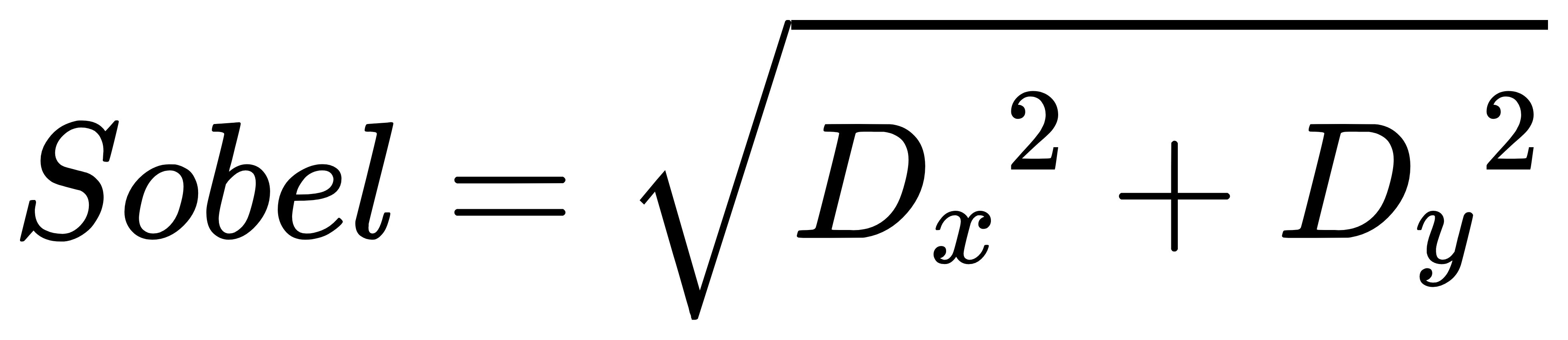
Prewitt:
- Prewitt算子在一个方向求微分,而在另一个方向求平均,因而对噪声相对不敏感,有抑制噪声的作用。但是像素平均相当于对图像的低通滤波,所以Prewitt算子对边缘的定位不如Roberts算子。
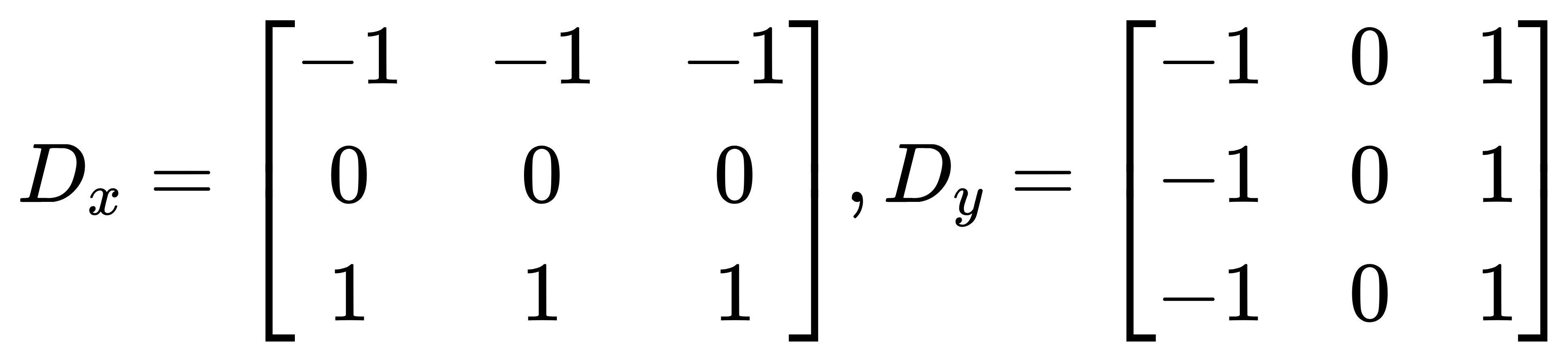
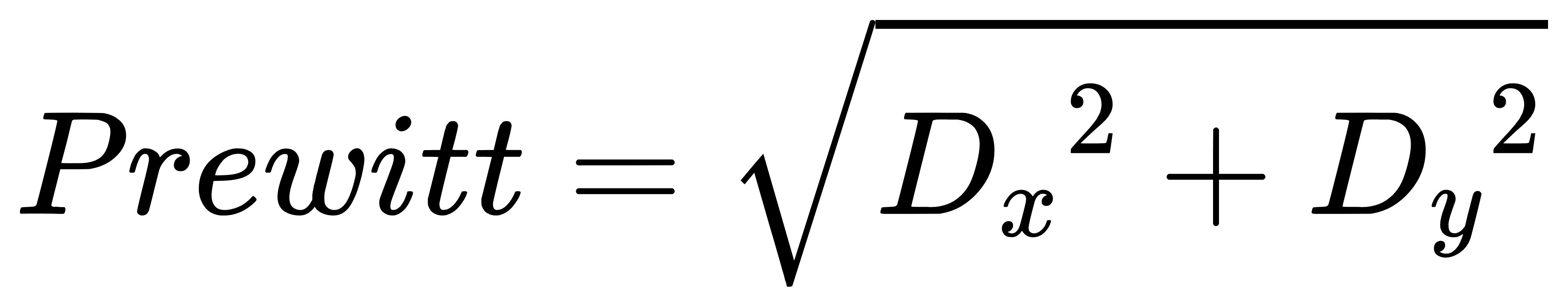
Laplace:
- Laplace算子是最简单的各向同性的二阶微分算子,是利用图像灰度二阶导数的零交叉点来求边缘点的算法。
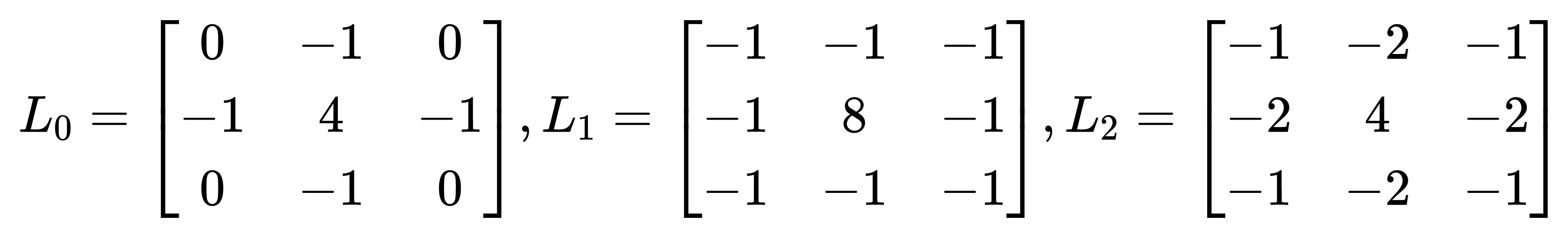
- Laplace算子检测边缘没有方向性,而且对噪声敏感,所以对于含噪声图像可以先滤除噪声再用Laplace算子检测边缘,也可以考虑采用将高斯滤波和Laplace边缘检测算子相结合的Log算检测边缘。
代码:
- 这个的效果更接近于单片机直接处理的结果
conv2的使用方法前面讲过
%edge use conv2
%read img
img = imread('B.jpg');
%2gray
gray = rgb2gray(img);
gray = imresize(gray,0.05);
%2double
gray = double(gray);
%Roberts
Roberts_D1 = [[-1,0] [0 1]] ;
Roberts_D2 = [[0 -1] [1 0]] ;
G1 = conv2(gray,Roberts_D1,'same');
G2 = conv2(gray,Roberts_D2,'same');
Roberts_o = abs(G1)+abs(G2);
%Sobel
Sobel_Dx = [[-1 -2 -1]
[ 0 0 0]
[ 1 2 1]];
Sobel_Dy = [[-1 0 1]
[-2 0 2]
[-1 0 1]];
Gx = conv2(gray,Sobel_Dx,'same');
Gy = conv2(gray,Sobel_Dy,'same');
Sobel_o = sqrt(Gx.*Gx + Gy.*Gy);
%Prewitt
Prewitt_Dx =[[-1 -1 -1]
[ 0 0 0]
[ 1 1 1]];
Prewitt_Dy =[[-1 0 1]
[-1 0 1]
[-1 0 1]];
Gx = conv2(gray,Prewitt_Dx,'same');
Gy = conv2(gray,Prewitt_Dy,'same');
Prewitt_o = sqrt(Gx.*Gx + Gy.*Gy);
%Laplace
L0 = [ [ 0 -1 0]
[-1 4 -1]
[ 0 -1 0] ];
L1 = [ [-1 -1 -1]
[-1 8 -1]
[-1 -1 -1] ];
L2 = [ [ 1 -2 1]
[-2 4 -2]
[ 1 -2 1] ];
Laplace_o = conv2(gray,L0,'same');
Laplace_o2 = conv2(gray,L1,'same');
Laplace_o3 = conv2(gray,L2,'same');
%2uint8
gray = uint8(gray);
Roberts_o = uint8(Roberts_o);
Sobel_o = uint8(Sobel_o);
Prewitt_o = uint8(Prewitt_o);
Laplace_o = uint8(Laplace_o);
Laplace_o2 = uint8(Laplace_o2);
Laplace_o3 = uint8(Laplace_o3);
%show
subplot(331);imshow(img);title("Orig");
subplot(332);imshow(gray);title('Gray');
subplot(334);imshow(Roberts_o);title("Roberts");
subplot(335);imshow(Prewitt_o);title('Prewitt');
subplot(336);imshow(Sobel_o);title("Sobel");
subplot(337);imshow(Laplace_o);title('Laplace L0');
subplot(338);imshow(Laplace_o2);title('Laplace L1');
subplot(339);imshow(Laplace_o3);title('Laplace L2');
效果:

- 图片尺寸缩小到了
92 * 205,与实际车车的相差不大
观察各个算子
- Roberts交叉微分算子计算量较小,需要两个2×2卷积后求和,效果还可以,对于一些细节(例如远处的红色障碍、右上角的赛道)处理不是很好
- Prewitt和Sobel算子计算量比较大,需要计算两个3×3卷积 并平方和再开方。效果确实是最好的,对于边界敏感,但也容易受图像噪声影响。
- Laplace算子是二阶微分算子,只需要计算一个3×3的卷积,代码中列举了L0 L1 L2三个算子,L1效果突出。
- 边缘检测输出图像可能还要再做后续处理,比如二值化,保存边线之类。有没有怨种学弟尝试一下是否可用。
0×04图像滤波(做实验的时候用的,做车好像用不上)
imnoise()
在Matlab中有一个重要的噪声生成函数imnoise,其常见语法说明如下:
| 语法 | 参数说明 |
|---|
| J = imnoise(I,type) | 按照给定类型添加图像噪声给图像I |
| J = imnoise(I,type,parameters) | parameters泛指可以添加的参数,类型不同,参数自然不同 |
| J = imnoise(I,‘gaussian’,m,v) | 添加高斯白噪声,均值为m,方差为v。default状态下,m = 0,v = 0.01 |
| J = imnoise(I,‘localvar’,V) | 添加零均值,局部方差为V的高斯白噪声给图像I。V是与I尺寸相同的数组 |
| J = imnoise(I,‘poisson’) | 添加Poisson噪声给图像I |
| J = imnoise(I,‘salt & pepper’,d) | 添加椒盐噪声给图像I,d是噪声密度。这将影响d * numel(I)个像素。default状态下,d = 0.05 |
| J = imnoise(I,‘speckle’,v) | 添加乘法噪声给图像I,v是方差。机理:J = I + n * I,n是均匀分布的随机噪声。在default状态下,v = 0.04 |
均值滤波

- 由于实验要求,并没有用现成的函数
%read img
img = imread('D.jpg');
img = rgb2gray(img);
img = imresize(img,0.4);
%add noise
gaus = imnoise(img,'gaussian');
spep = imnoise(img,'salt & pepper');
%2double
gaus = double(gaus);
spep = double(spep);
%set H
H =ones(3,3) * (1/9);
%
[hrow,hcol] = size(H);
drow = (hrow-1)/2;
dcol = (hcol-1)/2;
[row,col] = size(img);
new = zeros(row,col);
new2 = zeros(row,col);
for y = 1+drow:row-drow
for x = 1+dcol:col-dcol
mid = gaus(y-drow:y+drow,x-dcol:x+dcol).*H;
mid2 = spep(y-drow:y+drow,x-dcol:x+dcol).*H;
new(y,x) = sum(mid(:));
new2(y,x) = sum(mid2(:));
end
end
%2uint8
gaus = uint8(gaus);
spep = uint8(spep);
new = uint8(new);
new2 = uint8(new2);
%show
subplot(221);imshow(gaus);title("Gaussian");
subplot(222);imshow(new);title('GaussianOUT');
subplot(223);imshow(spep);title("salt & pepper’");
subplot(224);imshow(new2);title('spepOUT');
中值滤波

- 由于实验要求,并没有用现成的函数
%read img
img = imread('A.jpg');
img = rgb2gray(img);
img = imresize(img,0.1);
%add noise
gaus = imnoise(img,'gaussian');
spep = imnoise(img,'salt & pepper');
%2double
gaus = double(gaus);
spep = double(spep);
%
hrow = 5;
hcol = 5;
drow = (hrow-1)/2;
dcol = (hcol-1)/2;
[row,col] = size(img);
new1 = zeros(row,col);
new2 = zeros(row,col);
for y = 1+drow:row-drow
for x = 1+dcol:col-dcol
mid1 = gaus(y-drow:y+drow,x-dcol:x+dcol);
mid1 = sort(mid1(:));
mid2 = spep(y-drow:y+drow,x-dcol:x+dcol);
mid2 = sort(mid2(:));
new1(y,x) = mid1((hrow*hcol+1)/2);
new2(y,x) = mid2((hrow*hcol+1)/2);
end
end
%2uint8
gaus = uint8(gaus);
spep = uint8(spep);
new1 = uint8(new1);
new2 = uint8(new2);
%show
subplot(221);imshow(gaus);title("Gaussian");
subplot(222);imshow(new1);title('GaussianOUT');
subplot(223);imshow(spep);title("salt & pepper’");
subplot(224);imshow(new2);title('spepOUT');
K临近平滑滤波

- 由于实验要求,并没有用现成的函数
%K average
%read img
img = imread('C.jpg');
img = rgb2gray(img);
img = imresize(img,0.4);
%add noise
gaus = imnoise(img,'gaussian');
spep = imnoise(img,'salt & pepper');
%2double
gaus = double(gaus);
spep = double(spep);
%set H
%
hrow = 7;
hcol = 7;
k = 25;
drow = (hrow-1)/2;
dcol = (hcol-1)/2;
[row,col] = size(img);
new1 = zeros(row,col);
new2 = zeros(row,col);
near1 = zeros(1,k);
near2 = zeros(1,k);
for y = 1+drow:row-drow
for x = 1+dcol:col-dcol
mid1 = gaus(y-drow:y+drow,x-dcol:x+dcol);
n1 = mid1(1+drow,1+dcol);
[sort1,id1] = sort(abs(mid1(:)-n1));
for i = 1:k
near1(i) = mid1(id1(i)) ;
end
new1(y,x) = mean(near1);
mid2 = spep(y-drow:y+drow,x-dcol:x+dcol);
n2 = mid2(1+drow,1+dcol);
[sort2,id2] = sort(abs(mid2(:)-n2));
for i = 1:k
near2(i) = mid2(id2(i)) ;
end
new2(y,x) = mean(near2);
end
end
%2uint8
gaus = uint8(gaus);
spep = uint8(spep);
new1 = uint8(new1);
new2 = uint8(new2);
%show
subplot(221);imshow(gaus);title("Gaussian");
subplot(222);imshow(new1);title('GaussianOUT');
subplot(223);imshow(spep);title("salt & pepper’");
subplot(224);imshow(new2);title('spepOUT');
LaTex堆积处:
$$
g(x) = \left{\begin{matrix} \alpha f(i,j)\quad\qquad\qquad\qquad,0\le f(i,j)< f{a}
\ \beta [f(i,j)-f{a}]+g{a}\qquad,f{a}\le f(i,j) < f{b}
\ \gamma [f(i,j)-f{b}]+g{b}\qquad,f{b}\le f(i,j) < 255
\end{matrix}\right.
$$
$$
g(i,j) = c \cdot lg(1+f(i,j))
$$
$$
D{1} = \begin{bmatrix}
-1& 0\
0 & 1
\end{bmatrix},
D{2} = \begin{bmatrix}
0&-1\
1&0
\end{bmatrix}
$$
$$ Roberts = \left | D{1} \right | +\left | D{2}\right | $$
$$
D{x}=\begin{bmatrix}
-1 & -2 & -1\
0 & 0 & 0\
1 & 2 & 1
\end{bmatrix},
D{y}=\begin{bmatrix}
-1 & 0 & 1\
-2 & 0 & 2\
-1 & 0 & 1
\end{bmatrix}
$$
$$Sobel = \sqrt{{D{x}}^{2}+{D{y}}^{2}} $$
$$
D{x}=\begin{bmatrix}
-1 & -1 & -1\
0 & 0 & 0\
1 & 1 & 1
\end{bmatrix},
D{y}=\begin{bmatrix}
-1 & 0 & 1\
-1 & 0 & 1\
-1 & 0 & 1
\end{bmatrix}
$$
$$
Prewitt = \sqrt{{D{x}}^{2}+{D{y}}^{2}}
$$
$$
L{0} = \begin{bmatrix}
0 & -1 & 0\
-1 & 4 & -1\
0 & -1 & 0
\end{bmatrix} ,
L{1} = \begin{bmatrix}
-1 & -1 & -1\
-1 & 8 & -1\
-1 & -1 & -1
\end{bmatrix},
L_{2} = \begin{bmatrix}
-1 & -2 & -1\
-2 & 4 & -2\
-1 & -2 & -1
\end{bmatrix}
$$