Matlab遗传算法

YuTaov5

Matlab遗传算法

题目

步骤

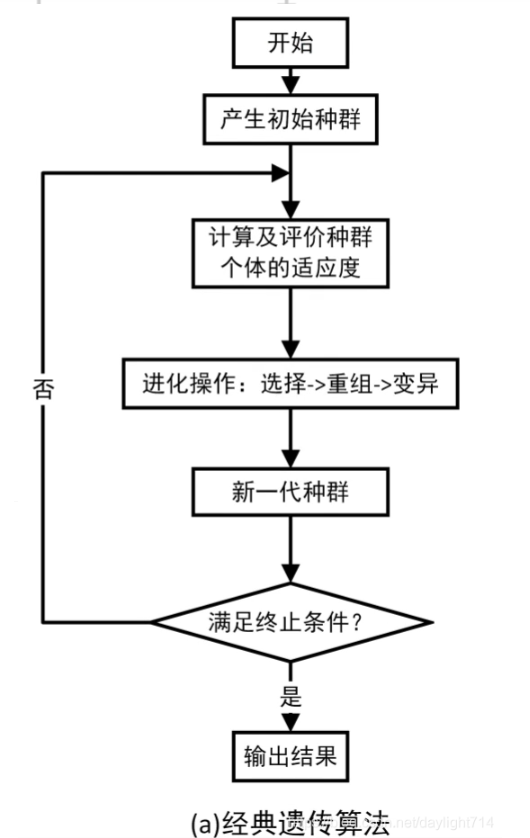
Matlab画图像

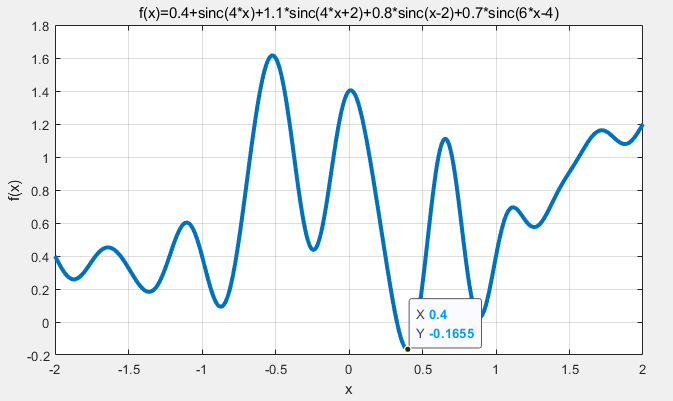
GeoGebra求极值

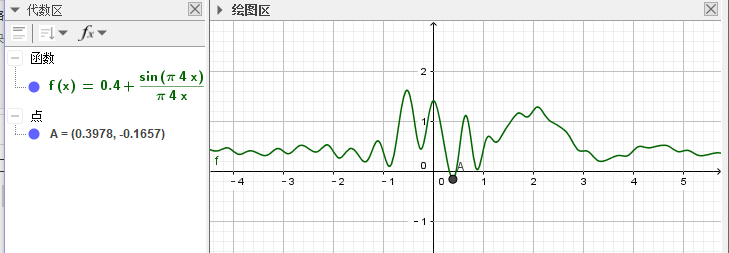
代码

%%%%%%%%先画图看看函数形状%%%%%%%%%%%%%%%%%
clear all;          %清除所有变量
close all;          %清图
clc;                %清屏
x=-2:0.01:2;
y=0.4+sinc(4*x)+1.1*sinc(4*x+2)+0.8*sinc(x-2)+0.7*sinc(6*x-4);
plot(x,y)
xlabel('x')
ylabel('f(x)')
title('f(x)=0.4+sinc(4*x)+1.1*sinc(4*x+2)+0.8*sinc(x-2)+0.7*sinc(6*x-4)')
%%%%%%%%标准遗传算法求函数极值%%%%%%%%%%
%%%%%%%%%%%初始化参数%%%%%%%%%%%%%%%%%%
clear all;       %清除所有变量
clc;             %清屏
NP=30;           %种群数量
L=16;            %二进制位串长度
Pc=0.3;          %交叉率
Pm=0.01;          %变异率
G=400;           %最大遗传代数
Xs=2;           %上限
Xx=-2;            %下限
f=randi([0,1],NP,L);%随机获得初始种群（二维数组）

%%%%%%%%遗传算法循环%%%%%%%%%%%%%%%%%%
for k=1:G
    %%%%%%%将二进制解码为定义域范围内十进制%%%%%%%
    for i=1:NP             %对种群中每个个体
        U=f(i,:);          %求种群中每个个体的染色体二进制编码数组
        m=0;            
        for j=1:L          %遍历某个个体的每一位
            m=U(j)*2^(j-1)+m;%求出该个体的二进制编码的十进制数
        end
        x(i)=Xx+m*(Xs-Xx)/(2^L-1);%映射到所要求的的自变量区间上
        Fit(i)=-func(x(i));%调用适应度函数
    end
    maxFit=max(Fit);       %定义适应度中的最小值
    minFit=min(Fit);       %定义适应度中的最小值
    rr=find(Fit==maxFit);  %返回适应度函数值组成的数组Fit中等于最小值的所有元素索引值组成的数组
    fBest=f(rr(1,1),:);    %得到第k代最优个体的染色体编码数组
    xBest=x(rr(1,1));      %得到最优个体对应十进制映射数值
    Fit=(Fit-minFit)/(maxFit-minFit);%归一化适应度函数值
     %%%%%%%基于轮盘赌的复制操作%%%%%%%%%%
    sum_Fit=sum(Fit);      %定义适应度函数值总和
    fitvalue=Fit./sum_Fit; %得到个体被选择概率数组=适应度函数值数组./适应度函数总和（轮盘赌）
    fitvalue=cumsum(fitvalue);%cumsum函数返回与原先同等维度和结构的累加和形式数组
    ms=sort(rand(NP,1));   %随机生成NP行1列的【0,1】范围小数的列向量并且升序排序
    fiti=1;                %计数变量，表示原种群中当前被比较的个体序号
    newi=1;                %计数变量，表示现在被选择进入下一代的个体序号
    while newi<=NP && fiti<=NP
        if (ms(newi))<fitvalue(fiti) %当ms随机数数组中第newi个随机小数小于适应度第fiti个累计值时
            nf(newi,:)=f(fiti,:);    %进行选择个体操作，生成子代种群nf第newi个个体并赋值染色体
            newi=newi+1;             %进入下一代个体数加1
        else
            fiti=fiti+1;             %若不满足，则该个体不被选择，进入下一个个体的判断
        end
    end
    %%%%%%%%基于概率的交叉操作%%%%%%%%
    for i=1:2:NP                     %步长为2，代表从原种群数组中选取相邻两个为一对考虑是否进行交叉操作
        p=rand;                      %生成【0,1】随机小数
        if p<Pc                      %若p小于交叉概率
            q=randi([0,1],1,L);      %生成一条（0,1）分布的二进制数串
            for j=1:L                %对该数串上的每一位
                if q(j)==1           %如果第j位上的值为1，则进行第i组个体的第j位交叉操作
                    temp=nf(i+1,j);  
                    nf(i+1,j)=nf(i,j);
                    nf(i,j)=temp;    %上三步完成了第j位交叉互换
                end
            end
        end
    end
    %%%%%%%%基于概率的变异操作%%%%%%%%%
    i=1;
    while i<=round(NP*Pm)        %round表示四舍五入法取整，表示总共要对NP*Pm个个体进行变异
        h=randi([1,NP],1,1);     %随机选取一条需要变异的染色体
        for j=1:round(L*Pm)      %在需要变异的某条染色体总共进行L*Pm个基因变异
            g=randi([1,L],1,1);  %随机选取需要变异的基因序号
            nf(h,g)=~nf(h,g);    %取反完成变异
        end
        i=i+1;
    end
    
    f=nf;                        
    f(1,:)=fBest;                %保留最优个体在新种群中
    trace(k)=-maxFit;             %把第k代最优适应度保存到数组trace中
end

disp(['最终函数最小值点为',num2str(xBest)])%循环结束后在命令行输出最后一代的最优个体对应的映射值
figure
plot(trace)                      %画图画出历代函数最小值（即适应度函数最小值）进化曲线
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')
x=xBest
y=-maxFit

%%%%%%%%适应度函数%%%%%%%%%%
function result=func(x)         %定义函数名为func和返回形式参数名为result的适应度函数
fit=0.4+sinc(4*x)+1.1*sinc(4*x+2)+0.8*sinc(x-2)+0.7*sinc(6*x-4);    %直接把目标函数作为适应度函数，这也就解释了为什么适应度最大就最优
result=fit;
end
结果

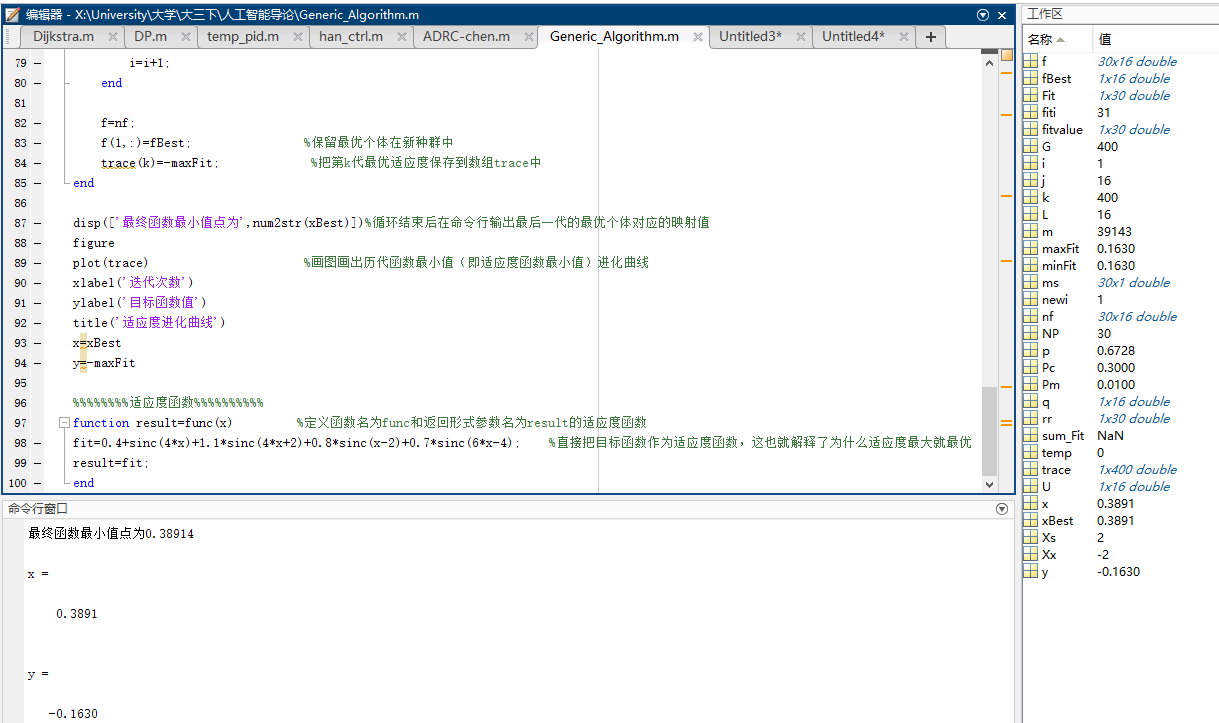
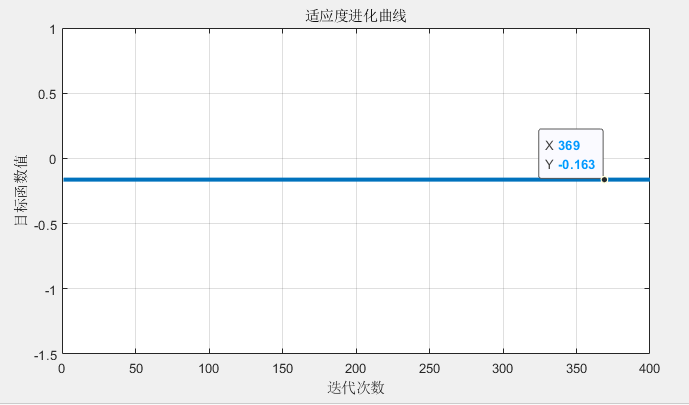
综上

Matlab算法运行结果-0.163与GeoGebra软件求出极值-0.1657很相近